::. Selamat Datang di Blog Matematika SMA .::

Jumat, 20 April 2012

Determinan

di 01.42
Diposting oleh A. S. Rohman
Determinan adalah suatu fungsi tertentu yang menghubungkan suatu bilangan real dengan suatu matriks bujursangkar.
Sebagai contoh, kita ambil matriks A2x2
A = \begin{bmatrix} a & b\\ c & d\\ \end{bmatrix}   determinan A     det(A)= ad-bc

Determinan dengan Minor dan kofaktor

A = \begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{bmatrix} tentukan determinan A
Pertama buat minor dari a11
M11 = \begin{bmatrix} a_{22} & a_{23}\\ a_{32} & a_{33}\\ \end{bmatrix} = detM = a22a33 x a23a32
Kemudian kofaktor dari a11 adalah
c11 = (-1)1+1M11 = (-1)1+1a22a33 x a23a32
kofaktor dan minor hanya berbeda tanda Cij=±Mij untuk membedakan apakah kofaktor pada ij adalah + atau - maka kita bisa melihat matrik dibawah ini
\begin{bmatrix} +&-&+&-&+&\cdots\\ -&+&-&+&-&\cdots\\ +&-&+&-&+&\cdots\\ -&+&-&+&-&\cdots\\ \vdots&\vdots&\vdots&\vdots&\vdots& \\ \end{bmatrix}
Begitu juga dengan minor dari a32
M32 = \begin{bmatrix} a_{11} & a_{13}\\ a_{21} & a_{23}\\ \end{bmatrix} = detM = a11a23 x a13a21
Maka kofaktor dari a32 adalah
c32 = (-1)3+2M32 = (-1)3+2 x a11a23 x a13a21
Secara keseluruhan, definisi determinan ordo 3x3 adalah
det(A) = a11C11+a12C12+a13C13

Determinan dengan Ekspansi Kofaktor Pada Baris Pertama

Misalkan ada sebuah matriks A3x3
A = \begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{bmatrix}
maka determinan dari matriks tersebut dengan ekspansi kofaktor adalah,
det(A) = a11\begin{bmatrix}a_{22} & a_{23}\\ a_{32} & a_{33}\\ \end{bmatrix} - a12\begin{bmatrix}a_{21} & a_{23}\\ a_{31} & a_{33}\\ \end{bmatrix} + a13\begin{bmatrix}a_{21} & a_{22}\\ a_{31} & a_{32}\\ \end{bmatrix}
= a11(a22a33 - a23a32) - a12(a21a33 - a23a31) + a13(a21a32 - a22a31)
= a11a22a33 + a12a23a31 + a13a21a32 - a13a22a31 - a12a21a33 - a11a23a32
Contoh Soal:
A = 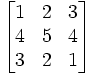\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 4\\ 3 & 2 & 1\\ \end{bmatrix} tentukan determinan A dengan metode ekspansi kofaktor baris pertama
Jawab:
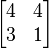det(A) = \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 4\\ 3 & 2 & 1\\ \end{bmatrix} = 1\begin{bmatrix} 5 & 4\\2 & 1\\ \end{bmatrix} - 2\begin{bmatrix} 4 & 4\\ 3 & 1\\ \end{bmatrix} + 3\begin{bmatrix} 4 & 5\\3 & 2\\ \end{bmatrix} = 1(-3) - 2(-8) + 3(-7) = -8

Adjoin Matriks 3 x 3

Bila ada sebuah matriks A3x3
A = \begin{bmatrix} 3&2&-1\\ 1&6&3 \\ 2&4&0\\ \end{bmatrix}
Kofaktor dari matriks A adalah
C11 = -12 C12 = 6 C13 = -8
C21 = -4 C22 = 2 C23 = -8
C31 = 12 C32 = -10 C33 = 8
maka matriks yang terbentuk dari kofaktor tersebut adalah
\begin{bmatrix} -12&6&-8\\ -4&2&-8\\ 12&-10&8\\ \end{bmatrix}
untuk mencari adjoint sebuah matriks, kita cukup mengganti kolom menjadi baris dan baris menjadi kolom
adj(A) = \begin{bmatrix} -12&-4&12\\ 6&2&-10\\ -8&-8&8\\ \end{bmatrix}

Determinan Matriks Segitiga Atas

Jika A adalah matriks segitiga nxn (segitiga atas, segitiga bawah atau segitiga diagonal) maka det(A) adalah hasil kali diagonal matriks tersebut
det(A) = a_{11}a_{22}\cdots a_{nn}
Contoh
\begin{bmatrix} 2&7&-3&8&3\\ 0&-3&7&5&1\\ 0&0&6&7&6\\ 0&0&0&9&8\\ 0&0&0&0&4\\ \end{bmatrix} = (2)(-3)(6)(9)(4) = -1296

Metode Cramer

jika Ax = b adalah sebuah sistem linear n yang tidak di ketahui dan det(A)≠ 0 maka persamaan tersebut mempunyai penyelesaian yang unik
X_{1} = \frac{det(A_{1})} {det(A)}, X_{2} = \frac{det(A_{2})} {det(A)}, ... , X_{n} = \frac{det(A_{n})} {det(A)}
dimana A j adalah matrik yang didapat dengan mengganti kolom j dengan matrik b
Contoh soal:
Gunakan metode cramer untuk menyelesaikan persoalan di bawah ini
x1 + 2x3 = 6
-3x1 + 4x2 + 6x3 = 30
-x1 - 2x2 + 3x3 = 8
Jawab:
bentuk matrik A dan b
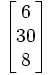
A = \begin{bmatrix} 1 & 0 & 2\\ -3 & 4 & 6\\ -1 & -2 & 3\\ \end{bmatrix} b = \begin{bmatrix} 6\\ 30\\ 8\\ \end{bmatrix}
kemudian ganti kolom j dengan matrik b
A1 = \begin{bmatrix} 6 & 0 & 2\\ 30 & 4 & 6\\ 8 & -2 & 3\\ \end{bmatrix} A2 = \begin{bmatrix} 1 & 6 & 2\\ -3 & 30 & 6\\ -1 & 8 & 3\\ \end{bmatrix} A3 = \begin{bmatrix} 1 & 0 & 6\\ -3 & 4 & 30\\ -1 & -2 & 8\\ \end{bmatrix}
dengan metode sarrus kita dapat dengan mudah mencari determinan dari matrik-matrik di atas
maka,
x_{1} = \frac{det(A_{1})} {det(A)} = \frac{-40} {44} = \frac{-10} {11}
x_{2} = \frac{det(A_{2})} {det(A)} = \frac{72} {44} = \frac{18} {11}
x_{3} = \frac{det(A_{3})} {det(A)} = \frac{152} {44} = \frac{38} {11}

R=Er...E2 E1 A
dan,
det(R)=det(Er)...det(E2)det(E1)det(EA)
Jika A dapat di-invers, maka sesuai dengan teorema equivalent statements , maka R = I, jadi det(R) = 1 ≠ 0 dan det(A) ≠ 0. Sebaliknya, jika det(A) ≠ 0, maka det(R) ≠ 0, jadi R tidak memiliki baris yang nol. Sesuai dengan teorema R = I, maka A adalah dapat di-invers. Tapi jika matrix bujur sangkar dengan 2 baris/kolom yang proposional adalah tidak dapat diinvers.
Contoh Soal :
A=\begin{bmatrix} 1 & 2 & 3\\ 1 & 0 & 1\\ 2 & 4 & 6\\ \end{bmatrix}
karena det(A) = 0. Maka A adalah dapat diinvers.

Mencari determinan dengan cara Sarrus

A = \begin{bmatrix} a & b & c\\ d & e & f\\ g & h & i\\ \end{bmatrix} tentukan determinan A
untuk mencari determinan matrik A maka,
detA = (aei + bfg + cdh) - (bdi + afh + ceg)

Metode Sarrus hanya untuk matrix berdimensi 3x3 Menghitung Inverse dari Matrix 3 x 3

A = \begin{bmatrix} 3 & 2 & -1\\ 1 & 6 & 3\\ 2 & -4 & 0\\ \end{bmatrix}
kemudian hitung kofaktor dari matrix A
C11 = 12 C12 = 6 C13 = -16
C21 = 4 C22 = 2 C23 = 16
C31 = 12 C32 = -10 C33 = 16
menjadi matrix kofaktor
\begin{bmatrix} 12 & 6 & -16\\ 4 & 2 & 16\\ 12 & -10 & 16\\ \end{bmatrix}
cari adjoint dari matrix kofaktor tadi dengan mentranspose matrix kofaktor di atas, sehingga menjadi
adj(A) = \begin{bmatrix} 12 & 4 & 12\\ 6 & 2 & -10\\ -16 & 16 & 16\\ \end{bmatrix}
A^{-1} = \frac{1}{det(A)}adj(A)
dengan metode Sarrus, kita dapat menghitung determinan dari matrix A
\mathit{det(A) = 64}
A^{-1} = \frac{1}{det(A)}adj(A) = \frac{1}{64} \begin{bmatrix} 12 & 4 & 12\\ 6 & 2 & -10\\ -16 & 16 & 16\\ \end{bmatrix} = \begin{bmatrix} \frac{12}{64} & \frac{4}{64} & \frac{12}{64}\\ \frac{6}{64} & \frac{2}{64} & -\frac{10}{64}\\ -\frac{16}{64} & \frac{16}{64} & \frac{16}{64}\\ \end{bmatrix}


posting by: Wikipedia bahasa Indonesia, ensiklopedia bebas


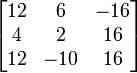
0 komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)

Info SNMPTN

PENDAFTARAN DAN TATA CARA PENDAFTARAN Pendaftaran dilakukan secara online dan tata cara pendaftaran secara lengkap dapat dilihat pada lamanhttp://ujian.snmptn.ac.id. Tatacara pengisian borang pendaftaran ujian tertulis dan keterampilan dapat diunduh (download) dari lamanhttp://download.snmptn.ac.id mulai tanggal 30 April 2012. Pendaftaran online dimulai dari tanggal 10 Mei 2012 pukul 08.00 WIB s.d 31 Mei 2012 pukul 22.00 WIB. JENIS UJIAN 1. Ujian Tertulis Ujian Tertulis terdiri dari: a. Tes Potensi Akademik (TPA) b. Tes Bidang Studi (TBS) Prediktif: i. Tes Bidang Studi Dasar terdiri atas mata ujian Matematika Dasar, Bahasa Indonesia, dan Bahasa Inggris. ii. Tes Bidang Studi IPA terdiri atas mata ujian Matematika, Biologi, Kimia, dan Fisika. iii. Tes Bidang Studi IPS terdiri atas mata ujian Sosiologi, Sejarah, Geografi, dan Ekonomi. 2. Ujian Keterampilan: Ujian Ketrampilan diperuntukkan bagi peminat: Program Studi bidang Ilmu Seni Program Studi bidang Ilmu Keolahragaan PENYELENGGARAAN UJIAN KETERAMPILAN UNTUK PROGRAM STUDI BIDANG ILMU SENI DAN BIDANG ILMU KEOLAHRAGAAN Peserta ujian yang memilih program studi bidang Ilmu Seni dan/atau Ilmu Keolahragaan diwajibkan mengikuti ujian keterampilan yang dilaksanakan pada tanggal 14 dan/atau 15 Juni 2012. Peserta Ujian dapat mengikuti Ujian Keterampilan di PTN yang memiliki program studi yang dipilih. Daftar PTN yang memiliki program studi penyelenggara ujian keterampilan secara lengkap dapat dilihat di laman http://www.snmptn.ac.id. JADWAL UJIAN Ujian Tertulis Selasa, 12 Juni 2012 : Tes Potensi Akademik dan Tes Bidang Studi Dasar Rabu, 13 Juni 2012 : Tes Bidang Studi IPA dan Tes Bidang Studi IPS Ujian Keterampilan Ujian Keterampilan dilaksanakan pada tanggal 14 dan/atau 15 Juni 2012. PENILAIAN HASIL UJIAN Penilaian hasil ujian menggunakan ketentuan sebagai berikut: Jawaban BENAR : + 4 Jawaban SALAH : - 1 Tidak Menjawab : 0 Penilaian dilakukan secara menyeluruh. Oleh karena itu, setiap mata ujian harus dikerjakan sebaik mungkin dan tidak ada yang diabaikan. KELOMPOK UJIAN Kelompok ujian tertulis SNMPTN terbagi menjadi 3 (tiga): a. Kelompok Ujian IPA b. Kelompok Ujian IPS c. Kelompok Ujian IPC Setiap peserta dapat mengikuti kelompok ujian IPA, IPS, atau IPC tidak harus sesuai dengan jurusan SMA/MA/SMK/MAK yang bersangkutan. KELOMPOK PROGRAM STUDI DAN JUMLAH PILIHAN Program Studi yang ada di PTN dibagi menjadi dua kelompok, yaitu Program Studi kelompok IPA dan IPS. Setiap peserta kelompok ujian IPA atau IPS dapat memilih maksimal 2 (dua) program studi sesuai dengan kelompok ujian yang diikuti. Setiap peserta kelompok ujian IPC dapat memilih maksimal 3 (tiga) program studi dengan catatan minimal satu program studi kelompok IPA dan satu program studi kelompok IPS. Urutan dalam pemilihan program studi menyatakan prioritas pilihan. Peserta ujian yang memilih hanya 1 (satu) program studi, pilihan program studi dapat dari PTN di Wilayah mana saja. Peserta ujian yang memilih 2 (dua) program studi atau lebih, salah satu pilihan program studi tersebut harus dari PTN yang berada dalam satu Wilayah dengan tempat peserta mengikuti ujian. Pilihan program studi yang lain dapat dari PTN di luar Wilayahnya. Daftar program studi, daya tampung tahun 2012, dan jumlah peminat tahun 2011 dapat dilihat di lamanhttp://www.snmptn.ac.id. BIAYA SELEKSI UJIAN TERTULIS DAN KETERAMPILAN Biaya seleksi Jalur Ujian Tertulis dan Keterampilan adalah : Rp.150.000,00 (Seratus lima puluh ribu rupiah) per peserta untuk kelompok IPA atau kelompok IPS. Rp.175.000,00 (Seratus tujuh puluh lima ribu rupiah) per peserta untuk kelompok IPC (IPA dan IPS). Rp.150.000,00 (Seratus lima puluh ribu rupiah) per peserta per ujian keterampilan bagi yang memilih program studi yang mempersyaratkan Jalur Ujian Keterampilan. Biaya ujian dibayarkan ke Bank Mandiri. Biaya yang sudah dibayarkan tidak dapat ditarik kembali dengan alasan apapun. PENGUMUMAN HASIL UJIAN Hasil ujian akan diumumkan pada hari Sabtu, 7 Juli 2012 mulai pukul 19.00 WIB dan dapat diakses di lamanhttp://www.snmptn.ac.id. PESERTA PELAMAR BIDIKMISI Calon peserta Bidikmisi terlebih dahulu mempelajari prosedur pendaftaran Bidikmisi melalui lamanhttp://bidikmisi.dikti.go.id. Calon peserta Bidikmisi terlebih dahulu harus mendaftar ke laman http://bidikmisi.dikti.go.id. Calon peserta Bidikmisi yang dinyatakan memenuhi persyaratan oleh Ditjen Dikti akan memperoleh KAP dan PIN untuk mendaftar SNMPTN Jalur Ujian Tertulis melalui laman http://ujian.snmptn.ac.id, tanpa harus membayar biaya ujian. Calon peserta Bidikmisi yang dinyatakan tidak memenuhi persyaratan seleksi Jalur Undangan atau dinyatakan tidak diterima melalui seleksi Jalur Undangan, maka KAP dan PIN dapat digunakan kembali untuk mendaftar SNMPTN Jalur Ujian Tertulis tanpa harus membayar biaya ujian. Apabila calon peserta Bidikmisi telah dinyatakan lulus melalui seleksi Jalur Undangan dan berkeinginan untuk mendaftar SNMPTN Jalur Ujian Tertulis, maka PIN yang telah diperoleh dinyatakan tidak berlaku dan yang bersangkutan harus membayar biaya ujian dengan menggunakan KAP yang telah diperoleh sebelumnya. LAMAN RESMI DAN ALAMAT PANITIA PELAKSANA Informasi resmi mengenai SNMPTN dapat diakses melalui laman resmi http://www.snmptn.ac.id. Informasi resmi lainnya juga dapat diperoleh melalui Twitter SNMPTN: @2012snmptn, Facebook (http://www.facebook.com/groups/snmptn), http://halo.snmptn.ac.id, dan call center: 08041450450 Alamat Panitia SNMPTN 2012: Direktorat Pendidikan, Gedung Rektorat ITB lantai 4, Jl. Tamansari No.64 Bandung 40116. Telp/Fax. (022) 2530689, e-mail: panitia@snmptn.ac.id. LAIN-LAIN Segala perubahan ketentuan yang berkaitan dengan pelaksanaan SNMPTN 2012 akan diinformasikan melalui laman SNMPTN 2012 dan menjadi bagian dari Prosedur Operasional Baku (POB) SNMPTN 2012.